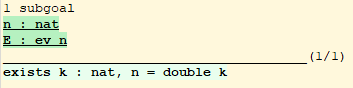Proof mode
Proof mode is used to prove theorems.
Rocq enters proof mode when you begin a proof,
such as with the Theorem command. It exits proof mode when
you complete a proof, such as with the Qed command. Tactics,
which are available only in proof mode, incrementally transform incomplete
proofs to eventually generate a complete proof.
When you run Rocq interactively, such as through RocqIDE, Proof General or
rocq repl, Rocq shows the current proof state (the incomplete proof) as you
enter tactics. This information isn't shown when you run Rocq in batch
mode with rocq compile.
Proof State
The proof state consists of one or more unproven goals. Each goal has a conclusion (the statement that is to be proven) and a local context, which contains named hypotheses (which are propositions), variables and local definitions that can be used in proving the conclusion. The proof may also use constants from the global environment such as definitions and proven theorems.
(Note that conclusion is also used to refer to the last part of an implication.
For example, in A -> B -> C, A and B are premises and C
is the conclusion.)
The term "goal" may refer to an entire goal or to the conclusion of a goal, depending on the context.
The conclusion appears below a line and the local context appears above the line.
The conclusion is a type. Each item in the local context begins with a name
and ends, after a colon, with an associated type.
Local definitions
are shown in the form n := 0 : nat, for example, in which nat is the
type of 0.
The local context of a goal contains items specific to the goal as well as section-local variables and hypotheses (see Assumptions) defined in the current section. The latter are included in the initial proof state. Items in the local context are ordered; an item can only refer to items that appear before it. (A more mathematical description of the local context is here.)
The global environment has definitions and proven theorems that are global in scope. (A more mathematical description of the global environment is here.)
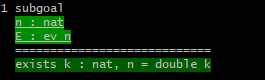
When you begin proving a theorem, the proof state shows the statement of the theorem below the line and often nothing in the local context:
- Parameter P: nat -> Prop.
- P is declared
- Goal forall n m: nat, n > m -> P 1 /\ P 2.
- 1 goal ============================ forall n m : nat, n > m -> P 1 /\ P 2
After applying the intros tactic, we see hypotheses above the line.
The names of variables (n and m) and hypotheses (H) appear before a colon, followed by
their type. The type doesn't have to be a provable statement.
For example, 0 = 1 and False are both valid and useful types.
- intros.
- 1 goal n, m : nat H : n > m ============================ P 1 /\ P 2
Some tactics, such as split, create new goals, which may
be referred to as subgoals for clarity.
Goals are numbered from 1 to N at each step of the proof to permit applying a
tactic to specific goals. The local context is only shown for the first goal.
- split.
- 2 goals n, m : nat H : n > m ============================ P 1 goal 2 is: P 2
"Variables" may refer specifically to local context items introduced
from forall variables for which the type of their type
is Set or Type. "Hypotheses" refers to items that are
propositions,
for which the type of their type is Prop or SProp,
but these terms are also used interchangeably.
- let t_n := type of n in idtac "type of n :" t_n; let tt_n := type of t_n in idtac "type of" t_n ":" tt_n.
- type of n : nat type of nat : Set
- let t_H := type of H in idtac "type of H :" t_H; let tt_H := type of t_H in idtac "type of" t_H ":" tt_H.
- type of H : (n > m) type of (n > m) : Prop
A proof script, consisting of the tactics that are applied to prove a theorem, is often informally referred to as a "proof". The real proof, whether complete or incomplete, is the associated term, the proof term, which users may occasionally want to examine. (This is based on the Curry-Howard isomorphism [Bar81, GLT89, How80, Hue89], which is a correspondence between between proofs and terms and between propositions and types of λ-calculus. The isomorphism is also sometimes called the "propositions-as-types correspondence".)
The Show Proof command displays the incomplete proof term
before you've completed the proof. For example, here's the proof
term after using the split tactic above:
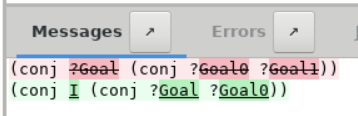
- Show Proof.
- (fun (n m : nat) (H : n > m) => conj ?Goal ?Goal0)
The incomplete parts, the goals, are represented by
existential variables
with names that begin with ?Goal. (Note that some existential variables
are not goals.) The Show Existentials command shows each existential with
the hypotheses and conclusion for the associated goal.
- Show Existentials.
- Existential 1 = ?Goal : [n : nat m : nat H : n > m |- P 1] Existential 2 = ?Goal0 : [n : nat m : nat H : n > m |- P 2]
Users can control which goals are displayed in the context by focusing goals. Focusing lets the user (initially) pick a single goal to work on. Focusing operations can be nested.
Tactics such as eapply create existential variables as placeholders for
undetermined variables that become shelved goals.
Shelved goals are not shown in the context by default, but they can be unshelved
to make them visible. Other tactics may automatically resolve these goals
(whether shelved or not); the purpose of shelving is to hide goals that the
user usually doesn't need to think about. See Existential variables
and this example.
Rocq's kernel verifies the correctness of proof terms when it exits proof mode by checking that the proof term is well-typed and that its type is the same as the theorem statement.
After a proof is completed, Print <theorem_name>
shows the proof term and its type. The type appears after
the colon (forall ...), as for this theorem from Rocq's standard library:
- Print proj1.
- Fetching opaque proofs from disk for Corelib.Init.Logic proj1 = fun (A B : Prop) (H : A /\ B) => match H with | conj x x0 => (fun (H0 : A) (_ : B) => H0) x x0 end : forall [A B : Prop], A /\ B -> A Arguments proj1 [A B]%_type_scope _
Note
Many tactics accept terms as arguments and frequently
refer to them with wording such as "the type of term".
When term is the name of a theorem or lemma, this wording
refers to the type of the proof term, which is what's given in the
Theorem statement. When term is the name of a hypothesis,
the wording refers to the type shown in the context for the hypothesis
(i.e., after the colon).
For terms that are more complex than just an ident,
you can use Check term to display their type.
Entering and exiting proof mode
Rocq enters proof mode when you begin a proof through
commands such as Theorem or Goal. Rocq user interfaces
usually have a way to indicate that you're in proof mode.
Tactics are available only in proof mode (currently they give syntax errors outside of proof mode). Most commands can be used both in and out of proof mode, but some commands only work in or outside of proof mode.
When the proof is completed, you can exit proof mode with commands such as
Qed, Defined and Save.
- Command Goal type
Asserts an unnamed proposition. This is intended for quick tests that a proposition is provable. If the proof is eventually completed and validated, you can assign a name with the
SaveorDefinedcommands. If no name is given, the name will beUnnamed_thm(or, if that name is already defined, a variant of that).
- Command Qed
Passes a completed proof term to Rocq's kernel to check that the proof term is well-typed and to verify that its type matches the theorem statement. If it's verified, the proof term is added to the global environment as an opaque constant using the declared name from the original goal.
It's very rare for a proof term to fail verification. Generally this indicates a bug in a tactic you used or that you misused some unsafe tactics.
- Error Attempt to save an incomplete proof.
- Error No focused proof (No proof-editing in progress).
You tried to use a proof mode command such as
Qedoutside of proof mode.
Note
Sometimes an error occurs when building the proof term, because tactics do not enforce completely the term construction constraints.
The user should also be aware of the fact that since the proof term is completely rechecked at this point, one may have to wait a while when the proof is large. In some exceptional cases one may even incur a memory overflow.
- Command Save ident
Similar to
Qed, except that the proof term is added to the global context with the nameident, which overrides any name provided by theTheoremcommand or its variants.
- Command Defined ident?
Similar to
QedandSave, except the proof is made transparent, which means that its content can be explicitly used for type checking and that it can be unfolded in conversion tactics (see Applying conversion rules,Opaque,Transparent). Ifidentis specified, the proof is defined with the given name, which overrides any name provided by theTheoremcommand or its variants.
- Command Admitted
This command is available in proof mode to give up the current proof and declare the initial goal as an axiom.
- Command Abort All?
Aborts the current proof. If the current proof is a nested proof, the previous proof becomes current. If
Allis given, all nested proofs are aborted. SeeNested Proofs Allowed.AllAborts all current proofs.
- Command Proof term
This command applies in proof mode. It is equivalent to
exact term. Qed.That is, you have to give the full proof in one gulp, as a proof term (see Section Applying theorems).Warning
Use of this command is discouraged. In particular, it doesn't work in Proof General because it must immediately follow the command that opened proof mode, but Proof General inserts
UnsetSilentbefore it (see Proof General issue #498).
- Command Proof
Is a no-op which is useful to delimit the sequence of tactic commands which start a proof, after a
Theoremcommand. It is a good practice to useProofas an opening parenthesis, closed in the script with a closingQed.See also
- Command Proof using section_var_expr with ltac_expr?
- section_var_expr
::=starred_ident_ref*|-? section_var_expr50section_var_expr50::=section_var_expr0 - section_var_expr0|section_var_expr0 + section_var_expr0|section_var_expr0section_var_expr0::=starred_ident_ref|()|( section_var_expr ) *?starred_ident_ref::=ident *?|Type *?|AllOpens proof mode, declaring the set of section variables (see Assumptions) used by the proof. These proof annotations are useful to enable asynchronous processing of proofs. This example shows how they work. The
Qedcommand verifies that the set of section variables used in the proof is a subset of the declared ones.The set of declared variables is closed under type dependency. For example, if
Tis a variable andais a variable of typeT, then the commandsProof using aandProof using T aare equivalent.The set of declared variables always includes the variables used by the statement. In other words
Proof using eis equivalent toProof using Type + efor any declaration expressione.- section_var_expr50Use all section variables except those specified by
section_var_expr50section_var_expr0 + section_var_expr0Use section variables from the union of both collections. See Name a set of section hypotheses for Proof using to see how to form a named collection.
section_var_expr0 - section_var_expr0Use section variables which are in the first collection but not in the second one.
*?Use the transitive closure of the specified collection.
TypeUse only section variables occurring in the statement. Specifying
*uses the forward transitive closure of all the section variables occurring in the statement. For example, if the variableHhas typep < 5thenHis inp*sincepoccurs in the type ofH.AllUse all section variables.
- Warning ident is both name of a Collection and Variable, Collection ident takes precedence over Variable.
If a specified name is ambiguous (it could be either a
Collectionor aVariable), then it is assumed to be aCollectionname.
- Warning Variable All is shadowed by Collection named All containing all variables.
This is variant of the previous warning for the All collection.
See also
- Attribute using
This attribute can be applied to the
Definition,Example,FixpointandCoFixpointcommands as well as toLemmaand its variants. It takes asection_var_expr, in quotes, as its value. This is equivalent to specifying the samesection_var_exprinProof using.Example
- Section Test.
- Variable n : nat.
- n is declared
- Hypothesis Hn : n <> 0.
- Hn is declared
- #[using="Hn"] Lemma example : 0 < n.
- 1 goal n : nat Hn : n <> 0 ============================ 0 < n
- Abort.
- End Test.
Example: Declaring section variables
When a section is closed with
End, section variables declared withProof usingare added to the theorem as additional variables. You can see the effect on the theorem's statement with commands such asCheck,Aboutafter the section is closed. Currently there is no command that shows the section variables associated with a theorem before the section is closed.Adding the unnecessary section variable
radixNotZerochanges howfoo'can be applied.
- Section bar.
- Variable radix : nat.
- radix is declared
- Hypothesis radixNotZero : 0 < radix.
- radixNotZero is declared
- Lemma foo : 0 = 0.
- 1 goal radix : nat radixNotZero : 0 < radix ============================ 0 = 0
- Proof. reflexivity. Qed.
- No more goals.
- Lemma foo' : 0 = 0.
- 1 goal radix : nat radixNotZero : 0 < radix ============================ 0 = 0
- Proof using radixNotZero. reflexivity. Qed. (* radixNotZero is not needed *)
- No more goals.
- Print foo'. (* Doesn't show radixNotZero yet *)
- foo' = eq_refl : 0 = 0 foo' uses section variables radix radixNotZero.
- End bar.
- Print foo. (* Doesn't change after the End *)
- foo = eq_refl : 0 = 0
- Print foo'. (* "End" added type radix (used by radixNotZero) and radixNotZero *)
- foo' = fun (radix : nat) (_ : 0 < radix) => eq_refl : forall radix : nat, 0 < radix -> 0 = 0 Arguments foo' radix%_nat_scope radixNotZero
- Goal 0 = 0.
- 1 goal ============================ 0 = 0
- Fail apply foo'. (* Fails because of the extra variable *)
- The command has indeed failed with message: Unable to find an instance for the variable radix.
- apply (foo' 5). (* Can be used if the extra variable is provided explicitly *)
- 1 goal ============================ 0 < 5
Proof using options
The following options modify the behavior of Proof using.
- Option Default Proof Using "section_var_expr"
Set this option to use
section_var_expras the defaultProof usingvalue. E.g.Set Default Proof Using "a b"will complete allProofcommands not followed by ausingpart withusing a b.Note that
section_var_exprisn't validated immediately. An invalid value will generate an error on a subsequentProoforQedcommand.
Name a set of section hypotheses for Proof using
- Command Collection ident := section_var_expr
This can be used to name a set of section hypotheses, with the purpose of making
Proof usingannotations more compact.Example
Define the collection named
Somecontainingx,yandz:Collection Some := x y z.
Define the collection named
Fewercontaining onlyxandy:Collection Fewer := Some - z
Define the collection named
Manycontaining the set union or set difference ofFewerandSome:Collection Many := Fewer + Some Collection Many := Fewer - Some
Define the collection named
Manycontaining the set difference ofFewerand the unnamed collectionx y:Collection Many := Fewer - (x y)
Deprecated since version 8.15: Redefining a collection, defining a collection with the same name as a variable, and invoking the
Proof usingcommand when collection and variable names overlap are deprecated. See the warnings below and in theProof usingcommand.- Error "All" is a predefined collection containing all variables. It can't be redefined.
When issuing a
Proof usingcommand, All used as a collection name always means "use all variables".
- Warning New Collection definition of ident shadows the previous one.
Redefining a
Collectionoverwrites the previous definition.
- Warning ident was already a defined Variable, the name ident will refer to Collection when executing "Proof using" command.
The
Proof usingcommand allows specifying bothCollectionandVariablenames. In case of ambiguity, a name is assumed to be Collection name.
Proof modes
When entering proof mode through commands such as Goal and Proof,
Rocq picks by default the Ltac mode. Nonetheless, there exist other proof modes
shipped in the standard Rocq installation, and furthermore some plugins define
their own proof modes. The default proof mode used when opening a proof can
be changed using the following option.
- Option Default Proof Mode string
This option selects the proof mode to use when starting a proof. Depending on the proof mode, various syntactic constructs are allowed when writing a proof. All proof modes support commands; the proof mode determines which tactic language and set of tactic definitions are available. The possible option values are:
"Classic"Activates the
Ltac language and the tactics with the syntax documented in this manual. Some tactics are not available until the associated plugin is loaded, such asSSRormicromega. This proof mode is set when the prelude is loaded."Noedit"No tactic language is activated at all. This is the default when the prelude is not loaded, e.g. through the
-noinitoption forrocq."Ltac2"Activates the Ltac2 language and the Ltac2-specific variants of the documented tactics. This value is only available after
RequiringLtac2.ImportingLtac2 sets this mode.
Some external plugins also define their own proof mode, which can be activated with this command.
Managing goals
- Command Undo To? natural?
Cancels the effect of the last
naturalcommands or tactics. TheTo naturalform goes back to the specified state number. Ifnaturalis not specified, the command goes back one command or tactic.
Focusing goals
Focusing lets you limit the context display to (initially) a
single goal. If a tactic creates additional goals from a focused goal, the
subgoals are also focused. The two focusing constructs are
curly braces ({ and }) and bullets
(e.g. -, + or *). These constructs can be nested.
Curly braces
- Tactic natural[ ident ] :? {
- Tactic }
{(without a terminating period) focuses on the first goal. The subproof can only be unfocused when it has been fully solved (i.e., when there is no focused goal left). Unfocusing is then handled by}(again, without a terminating period). See also an example in the next section.Note that when a focused goal is proved a message is displayed together with a suggestion about the right bullet or
}to unfocus it or focus the next goal.
[ ident ]: {Focuses on the goal named
identeven if the goal is not in focus. Goals are existential variables, which don't have names by default. You can give a name to a goal by usingrefine ?[ident].Example: Working with named goals
- Ltac name_goal name := refine ?[name]. (* for convenience *)
- name_goal is defined
- Set Printing Goal Names. (* show goal names, e.g. "(?base)" and "(?step)" *)
- Goal forall n, n + 0 = n.
- 1 goal (?Goal) ============================ forall n : nat, n + 0 = n
- Proof.
- induction n; [ name_goal base | name_goal step ].
- 2 goals, goal 1 (?base) ============================ 0 + 0 = 0 goal 2 (?step) is: S n + 0 = S n
- (* focus on the goal named "base" *)
- [base]: { reflexivity.
- 1 goal (?base) ============================ 0 + 0 = 0 This subproof is complete, but there are some unfocused goals. Try unfocusing with "}". 1 goal goal 1 (?step) is: S n + 0 = S n
- }
- 1 goal (?step) n : nat IHn : n + 0 = n ============================ S n + 0 = S n
This can also be a way of focusing on a shelved goal, for instance:
- Goal exists n : nat, n = n.
- 1 goal ============================ exists n : nat, n = n
- eexists ?[x].
- 1 focused goal (shelved: 1) ============================ ?x = ?x
- reflexivity.
- All the remaining goals are on the shelf. 1 goal goal 1 is: nat
- [x]: exact 0.
- No more goals.
- Qed.
- Error This proof is focused, but cannot be unfocused this way.
You are trying to use
}but the current subproof has not been fully solved.
- Error Brackets do not support multi-goal selectors.
Brackets are used to focus on a single goal given either by its position or by its name if it has one.
See also
The error messages for bullets below.
Bullets
Alternatively, proofs can be structured with bullets instead of { and }. The
first use of a bullet b focuses on the first goal g. The
same bullet can't be used again until the proof of g is completed,
then the next goal must be focused with another b. Thus,
all the goals present just before the first use of the bullet must be focused with the
same bullet b. See the example below.
Different bullets can be used to nest levels. The scope of each bullet
is limited to the enclosing { and }, so bullets can be reused as further
nesting levels provided they are delimited by curly braces. A bullet
is made from -, + or * characters (with no spaces and no period afterward):
- Tactic -+++*+
When a focused goal is proved, Rocq displays a message suggesting use of
} or the correct matching bullet to unfocus the goal or focus the next subgoal.
Note
In Proof General (Emacs interface to Rocq), you must use
bullets with the priority ordering shown above to have correct
indentation. For example - must be the outer bullet and + the inner
one in the example below.
Example: Use of bullets
For the sake of brevity, the output for this example is summarized in comments. Note that the tactic following a bullet is frequently put on the same line with the bullet. Observe that this proof still works even if all the bullets in it are omitted.
- Goal (1=1 /\ 2=2) /\ 3=3.
- 1 goal ============================ (1 = 1 /\ 2 = 2) /\ 3 = 3
- Proof.
- split. (* 1 = 1 /\ 2 = 2 and 3 = 3 *)
- 2 goals ============================ 1 = 1 /\ 2 = 2 goal 2 is: 3 = 3
- - (* 1 = 1 /\ 2 = 2 *)
- 1 goal ============================ 1 = 1 /\ 2 = 2
- split. (* 1 = 1 and 2 = 2 *)
- 2 goals ============================ 1 = 1 goal 2 is: 2 = 2
- + (* 1 = 1 *)
- 1 goal ============================ 1 = 1
- trivial. (* subproof complete *)
- This subproof is complete, but there are some unfocused goals. Focus next goal with bullet +. 2 goals goal 1 is: 2 = 2 goal 2 is: 3 = 3
- + (* 2 = 2 *)
- 1 goal ============================ 2 = 2
- trivial. (* subproof complete *)
- This subproof is complete, but there are some unfocused goals. Focus next goal with bullet -. 1 goal goal 1 is: 3 = 3
- - (* 3 = 3 *)
- 1 goal ============================ 3 = 3
- trivial. (* No more subgoals *)
- No more goals.
- Qed.
- Error Wrong bullet bullet1: Current bullet bullet2 is not finished.
Before using bullet
bullet1again, you should first finish proving the current focused goal. Note thatbullet1andbullet2may be the same.
- Error Wrong bullet bullet1: Bullet bullet2 is mandatory here.
You must put
bullet2to focus on the next goal. No other bullet is allowed here.
- Error No such goal. Focus next goal with bullet bullet.
You tried to apply a tactic but no goals were under focus. Using
bulletis mandatory here.
- Error No such goal. Try unfocusing with }.
You just finished a goal focused by
{, you must unfocus it with}.
Note
Use Default Goal Selector with the ! selector to force
the use of focusing mechanisms (bullets, braces) and goal selectors so
that it is always explicit to which goal(s) a tactic is applied.
Other focusing commands
- Command Unfocused
Succeeds if there are no unfocused goals. Otherwise the command fails.
- Command Focus natural?
Focuses the attention on the first goal to prove or, if
naturalis specified, thenatural-th. The printing of the other goals is suspended until the focused goal is solved or unfocused.Deprecated since version 8.8: Prefer the use of bullets or focusing braces with a goal selector (see above).
Shelving goals
Goals can be shelved so they are no longer displayed in the proof state.
Shelved goals can be unshelved with the Unshelve command, which
makes all shelved goals visible in the proof state. You can use
the goal selector [ ident ]: { to focus on a single shelved goal
(see here). Currently there's no single command or
tactic that unshelves goals by name.
- Tactic shelve
Moves the focused goals to the shelf. They will no longer be displayed in the context. The
Show Existentialscommand will still show these goals, which will be marked "(shelved)".
- Tactic shelve_unifiable
Shelves only the goals under focus that are mentioned in other goals. Goals that appear in the type of other goals can be solved by unification.
Example: shelve_unifiable
- Goal exists n, n=0.
- 1 goal ============================ exists n : nat, n = 0
- refine (ex_intro _ _ _).
- 1 focused goal (shelved: 1) ============================ ?Goal = 0
- all: shelve_unifiable.
- reflexivity.
- No more goals.
- Command Unshelve
This command moves all the goals on the shelf (see
shelve) from the shelf into focus, by appending them to the end of the current list of focused goals.
- Tactic unshelve ltac_expr1
Performs
tactic, then unshelves existential variables added to the shelf by the execution oftactic, prepending them to the current goal.
- Tactic admit
- Tactic give_up
Allows skipping a subgoal to permit further progress on the rest of the proof. The selected goals are removed from the context. They are not solved and cannot be solved later in the proof. Since the goals are not solved, the proof cannot be closed with
Qedbut only withAdmitted.
Reordering goals
- Tactic cycle int_or_var
Reorders the selected goals so that the first
integergoals appear after the other selected goals. Ifintegeris negative, it puts the lastintegergoals at the beginning of the list. The tactic is only useful with a goal selector, most commonlyall:. Note that other selectors reorder goals;1,3: cycle 1is not equivalent toall: cycle 1. See… : … (goal selector).Example: cycle
- Parameter P : nat -> Prop.
- P is declared
- Goal P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5.
- 1 goal ============================ P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5
- repeat split. (* P 1, P 2, P 3, P 4, P 5 *)
- 5 goals ============================ P 1 goal 2 is: P 2 goal 3 is: P 3 goal 4 is: P 4 goal 5 is: P 5
- all: cycle 2. (* P 3, P 4, P 5, P 1, P 2 *)
- 5 goals ============================ P 3 goal 2 is: P 4 goal 3 is: P 5 goal 4 is: P 1 goal 5 is: P 2
- all: cycle -3. (* P 5, P 1, P 2, P 3, P 4 *)
- 5 goals ============================ P 5 goal 2 is: P 1 goal 3 is: P 2 goal 4 is: P 3 goal 5 is: P 4
- Tactic swap int_or_var int_or_var
Exchanges the position of the specified goals. Negative values for
integerindicate counting goals backward from the end of the list of selected goals. Goals are indexed from 1. The tactic is only useful with a goal selector, most commonlyall:. Note that other selectors reorder goals;1,3: swap 1 3is not equivalent toall: swap 1 3. See… : … (goal selector).Example: swap
- Goal P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5.
- 1 goal ============================ P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5
- repeat split. (* P 1, P 2, P 3, P 4, P 5 *)
- 5 goals ============================ P 1 goal 2 is: P 2 goal 3 is: P 3 goal 4 is: P 4 goal 5 is: P 5
- all: swap 1 3. (* P 3, P 2, P 1, P 4, P 5 *)
- 5 goals ============================ P 3 goal 2 is: P 2 goal 3 is: P 1 goal 4 is: P 4 goal 5 is: P 5
- all: swap 1 -1. (* P 5, P 2, P 1, P 4, P 3 *)
- 5 goals ============================ P 5 goal 2 is: P 2 goal 3 is: P 1 goal 4 is: P 4 goal 5 is: P 3
- Tactic revgoals
Reverses the order of the selected goals. The tactic is only useful with a goal selector, most commonly
all :. Note that other selectors reorder goals;1,3: revgoalsis not equivalent toall: revgoals. See… : … (goal selector).Example: revgoals
- Goal P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5.
- 1 goal ============================ P 1 /\ P 2 /\ P 3 /\ P 4 /\ P 5
- repeat split. (* P 1, P 2, P 3, P 4, P 5 *)
- 5 goals ============================ P 1 goal 2 is: P 2 goal 3 is: P 3 goal 4 is: P 4 goal 5 is: P 5
- all: revgoals. (* P 5, P 4, P 3, P 2, P 1 *)
- 5 goals ============================ P 5 goal 2 is: P 4 goal 3 is: P 3 goal 4 is: P 2 goal 5 is: P 1
Proving a subgoal as a separate lemma: abstract
- Tactic abstract ltac_expr2 using identname?
Does a
solve[ ltac_expr2 ]and saves the subproof as an auxiliary lemma. ifidentnameis specified, the lemma is saved with that name; otherwise the lemma is saved with the nameident_subproofnatural?whereidentis the name of the current goal (e.g. the theorem name) andnaturalis chosen to get a fresh name. If the proof is closed withQed, the auxiliary lemma is inlined in the final proof term.This is useful with tactics such as
discriminatethat generate huge proof terms with many intermediate goals. It can significantly reduce peak memory use. In most cases it doesn't have a significant impact on run time. One case in which it can reduce run time is when a tacticfoois known to always pass type checking when it succeeds, such as in reflective proofs. In this case, the idiom "abstractexact_no_checkfoo" will save half the type checking type time compared to "exactfoo".Warning
The abstract tactic, while very useful, still has some known limitations. See #9146 for more details. We recommend caution when using it in some "non-standard" contexts. In particular,
abstractdoesn't work properly when used inside quotationsltac:(...). If used as part of typeclass resolution, it may produce incorrect terms when in polymorphic universe mode.Warning
Provide
identnameat your own risk; explicitly named and reused subterms don’t play well with asynchronous proofs.- Tactic transparent_abstract ltac_expr3 using ident?
Like
abstract, but save the subproof in a transparent lemma with a name in the formident_subtermnatural?.Warning
Use this feature at your own risk; building computationally relevant terms with tactics is fragile, and explicitly named and reused subterms don’t play well with asynchronous proofs.
- Error Proof is not complete.
Requesting information
- Command Show identnatural?
Displays the current goals.
naturalDisplay only the
natural-th goal.identDisplays the named goal
ident. This is useful in particular to display a shelved goal but only works if the corresponding existential variable has been named by the user (see Existential variables) as in the following example.Example
- Goal exists n, n = 0.
- 1 goal ============================ exists n : nat, n = 0
- eexists ?[n].
- 1 focused goal (shelved: 1) ============================ ?n = 0
- Show n.
- goal n is: ============================ nat
- Error No focused proof.
- Error No such goal.
- Command Show Proof Diffs removed??
Displays the proof term generated by the tactics that have been applied so far. If the proof is incomplete, the term will contain holes, which correspond to subterms which are still to be constructed. Each hole is an existential variable, which appears as a question mark followed by an identifier.
Specifying “Diffs” highlights the difference between the current and previous proof step. By default, the command shows the output once with additions highlighted. Including “removed” shows the output twice: once showing removals and once showing additions. It does not examine the
Diffsoption. See "Show Proof" differences.
- Command Show Conjectures
Prints the names of all the theorems that are currently being proved. As it is possible to start proving a previous lemma during the proof of a theorem, there may be multiple names.
- Command Show Intro
If the current goal begins by at least one product, prints the name of the first product as it would be generated by an anonymous
intro. The aim of this command is to ease the writing of more robust scripts. For example, with an appropriate Proof General macro, it is possible to transform any anonymousintrointo a qualified one such asintro y13. In the case of a non-product goal, it prints nothing.
- Command Show Existentials
Displays all open goals / existential variables in the current proof along with the context and type of each variable.
- Command Show Match qualid
Displays a template of the Gallina
matchconstruct with a branch for each constructor of the typequalid. This is used internally by company-coq.Example
- Show Match nat.
- match # with | O => | S x => end
- Error Unknown inductive type.
- Command Show Universes
Displays the set of all universe constraints and its normalized form at the current stage of the proof, useful for debugging universe inconsistencies.
- Command Show Goal natural at natural
Available in
rocq repl. Displays a goal at a proof state using the goal ID number and the proof state ID number. It is primarily for use by tools such as Prooftree that need to fetch goal history in this way. Prooftree is a tool for visualizing a proof as a tree that runs in Proof General.
- Command Guarded
Some tactics (e.g.
refine) allow to build proofs using fixpoint or cofixpoint constructions. Due to the incremental nature of proof construction, the check of the termination (or guardedness) of the recursive calls in the fixpoint or cofixpoint constructions is postponed to the time of the completion of the proof.The command
Guardedallows checking if the guard condition for fixpoint and cofixpoint is violated at some time of the construction of the proof without having to wait the completion of the proof.
Showing differences between proof steps
Rocq can automatically highlight the differences between successive proof steps
and between values in some error messages. Rocq can also highlight differences
in the proof term.
For example, the following screenshots of RocqIDE and coqtop show the application
of the same intros tactic. The tactic creates two new hypotheses, highlighted in green.
The conclusion is entirely in pale green because although it’s changed, no tokens were added
to it. The second screenshot uses the "removed" option, so it shows the conclusion a
second time with the old text, with deletions marked in red. Also, since the hypotheses are
new, no line of old text is shown for them.
This image shows an error message with diff highlighting in RocqIDE:
How to enable diffs
- Option Diffs "on""off""removed"
This option is used to enable diffs. The “on” setting highlights added tokens in green, while the “removed” setting additionally reprints items with removed tokens in red. Unchanged tokens in modified items are shown with pale green or red. Diffs in error messages use red and green for the compared values; they appear regardless of the setting. (Colors are user-configurable.)
For rocq repl, showing diffs can be enabled when starting rocq repl with the
-diffs on|off|removed command-line option or by setting the Diffs option
within Rocq. You will need to provide the -color on|auto command-line option when
you start rocq repl in either case.
Colors for rocq repl can be configured by setting the ROCQ_COLORS environment
variable. See section Environment variables. Diffs
use the tags diff.added, diff.added.bg, diff.removed and diff.removed.bg.
In RocqIDE, diffs should be enabled from the View menu. Don’t use the Set Diffs
command in RocqIDE. You can change the background colors shown for diffs from the
Edit | Preferences | Tags panel by changing the settings for the diff.added,
diff.added.bg, diff.removed and diff.removed.bg tags. This panel also
lets you control other attributes of the highlights, such as the foreground
color, bold, italic, underline and strikeout.
Proof General, VsCoq and Coqtail can also display Rocq-generated proof diffs automatically. Please see the PG documentation section "Showing Proof Diffs" and Coqtail's "Proof Diffs" for details.
How diffs are calculated
Diffs are calculated as follows:
Select the old proof state to compare to, which is the proof state before the last tactic that changed the proof. Changes that only affect the view of the proof, such as
all: swap 1 2, are ignored.For each goal in the new proof state, determine what old goal to compare it to—the one it is derived from or is the same as. Match the hypotheses by name (order is ignored), handling compacted items specially.
For each hypothesis and conclusion (the “items”) in each goal, pass them as strings to the lexer to break them into tokens. Then apply the Myers diff algorithm [Mye86] on the tokens and add appropriate highlighting.
Notes:
Aside from the highlights, output for the "on" option should be identical to the undiffed output.
Goals completed in the last proof step will not be shown even with the "removed" setting.
This screenshot shows the result of applying a split tactic that replaces one goal
with 2 goals. Notice that the goal P 1 is not highlighted at all after
the split because it has not changed.
Diffs may appear like this after applying a intro tactic that results
in a compacted hypotheses:
"Show Proof" differences
To show differences in the proof term:
In
rocq repland Proof General, use theShow ProofDiffscommand.In RocqIDE, position the cursor on or just after a tactic to compare the proof term after the tactic with the proof term before the tactic, then select
View / Show Prooffrom the menu or enter the associated key binding. Differences will be shown applying the currentShow Diffssetting from theViewmenu. If the current setting isDon't show diffs, diffs will not be shown.Output with the "added and removed" option looks like this:
Delaying solving unification constraints
- Tactic solve_constraints
- Flag Solve Unification Constraints
By default, after each tactic application, postponed typechecking unification problems are resolved using heuristics. Unsetting this flag disables this behavior, allowing tactics to leave unification constraints unsolved. Use the
solve_constraintstactic at any point to solve the constraints.
Proof maintenance
Experimental. Many tactics, such as intros, can automatically generate names, such
as "H0" or "H1" for a new hypothesis introduced from a goal. Subsequent proof steps
may explicitly refer to these names. However, future versions of Rocq may not assign
names exactly the same way, which could cause the proof to fail because the
new names don't match the explicit references in the proof.
The following Mangle Names settings let users find all the
places where proofs rely on automatically generated names, which can
then be named explicitly to avoid any incompatibility. These
settings cause Rocq to generate different names, producing errors for
references to automatically generated names.
- Flag Mangle Names
When this flag is set (it is off by default), generated names use the prefix specified in the following option instead of the default prefix.
- Flag Mangle Names Light
When this flag is set (it is off by default), the names generated by
Mangle Namesonly add theMangle Names Prefixto the original name.
Controlling proof mode
- Option Hyps Limit natural
This option controls the maximum number of hypotheses displayed in goals after the application of a tactic. All the hypotheses remain usable in the proof development. When unset, it goes back to the default mode which is to print all available hypotheses.
- Flag Nested Proofs Allowed
When turned on (it is off by default), this flag enables support for nested proofs: a new assertion command can be inserted before the current proof is finished, in which case Rocq will temporarily switch to the proof of this nested lemma. When the proof of the nested lemma is finished (with
QedorDefined), its statement will be made available (as if it had been proved before starting the previous proof) and Rocq will switch back to the proof of the previous assertion.
- Flag Printing Goal Names
When this flag is turned on, the name of the goal is printed in proof mode, which can be useful in cases of cross references between goals.
- Flag Printing Goal Tags
Internal flag used to implement Proof General's proof-tree mode.
Controlling memory usage
- Command Print Debug GC
Prints heap usage statistics, which are values from the
stattype of theGcmodule described here in the OCaml documentation. Thelive_words,heap_wordsandtop_heap_wordsvalues give the basic information. Words are 8 bytes or 4 bytes, respectively, for 64- and 32-bit executables.
When experiencing high memory usage the following commands can be used to force Rocq to optimize some of its internal data structures.
- Command Optimize Proof
Shrink the data structure used to represent the current proof.
- Command Optimize Heap
Perform a heap compaction. This is generally an expensive operation. See: OCaml Gc.compact There is also an analogous tactic
optimize_heap.
Memory usage parameters can be set through the OCAMLRUNPARAM environment variable.